Um es vorweg zu nehme, die Quantentheorie ist nicht aus dem
Hirn von Einstein entsprungen, sondern eher das Ergebnis vieler Ideen und
Beiträge (u.a. auch von Einstein) der unterschiedlichsten Physiker. Anfang
des 20. Jahrhunderts, als die Quantentheorie das Gehen lernte, revolutionierte
Einstein mit seiner Relativitätstheorie die Physik von Grund auf. Aus dem
vorsichtigen „Quanten-Gang“ wurde jedoch schnell eine zweite Revolution, die
Einstein jedoch nur wenig schmeckte. Sein berühmter Ausspruch „Gott würfelt
nicht“ bezieht sich auf teilweise unvorhersagbare Ereignisse der
Quantentheorie. Kennt man z.B. Ort und Impuls eines Planeten , so kann man mit
Hilfe der Allgemeinen Relativitätstheorie Ort und Impuls des Planeten zu einem
späteren Zeitpunkt vorhersagen. In der Quantentheorie funktionuckelt dies im übertragenden
Sinne, z.B. auf das Elektron eines Wasserstoffatoms aufgrund der Unschärferelation
nicht. Einstein gefiel der Gedanke nicht, dass man bezüglich Ort und Impuls
eines Quanten-Teilchens nur Wahrscheinlichkeitsaussagen treffen kann, also die
Bahn (wenn man überhaupt noch davon sprechen kann) des Teilchens nicht
vorhersagbar ist. Die Quantentheorie musste zwangsläufig erfunden bzw. gefunden
werden, da sich manchmal Teilchen bzw. Wellen wie Wellen bzw. Teilchen
verhalten. Dass sich Licht wie eine Welle verhält, leuchtet jedem ein, aber es kann sich
manchmal auch wie ein Teilchen verhalten. Man spricht vom
Welle-Teilchen-Dualismus. Die Frage ist, wann verhält sich das Licht wie eine
Welle und wann wie ein Teilchen? Das hängt vom Experiment ab. Hierzu ein paar
Beispiele:
Beugung des Lichtes (z.B. am Spalt oder Gitter) (Welleneigenschaft des Lichtes).
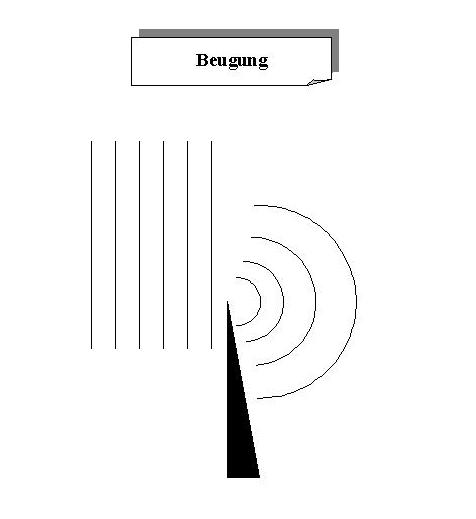
Die einlaufende ebene Welle wird an der scharfen Kante gebeugt.
Brechung des Lichtes (z.B. beim übergang vom dünneren ins dichtere Medium) (Welleneigenschaft des Lichtes).
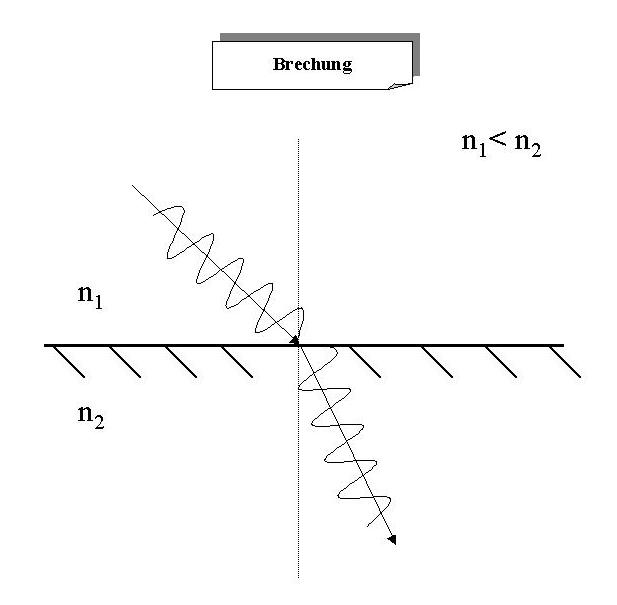
Das Licht wird beim übergang vom dünneren Medium (Brechungsindex n
1) ins dichtere (Brechungsindex n
2) zum Lot hin gebrochen.
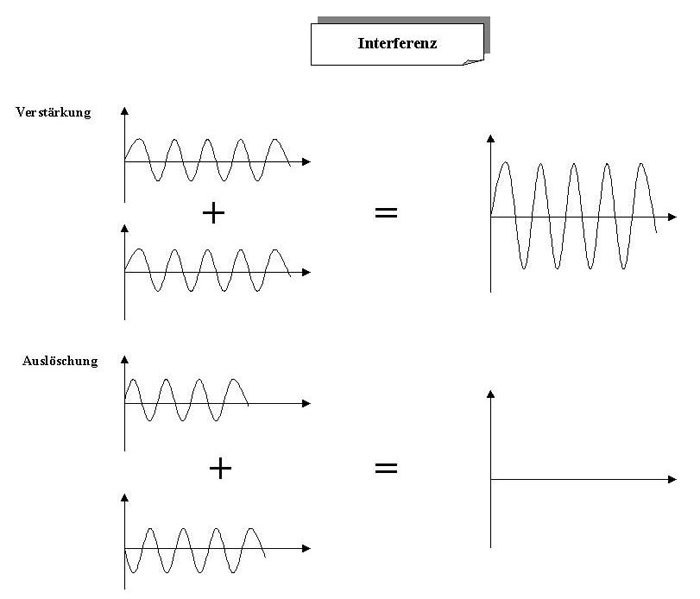
Interferenz von Licht (Welleneigenschaft des Lichtes).
Fotoeffekt (Absorbtion eines Lichtteilchens = Photons = Lichtquants mit der Energie
, h: Plancksches Wirkungsquantum,
Frequenz des Lichtes) (Teilcheneigenschaft des Lichtes).
Compton-Effekt Streuung eines Lichtquants z.B. an einem Elektron (Teilcheneigenschaft des Lichtes).
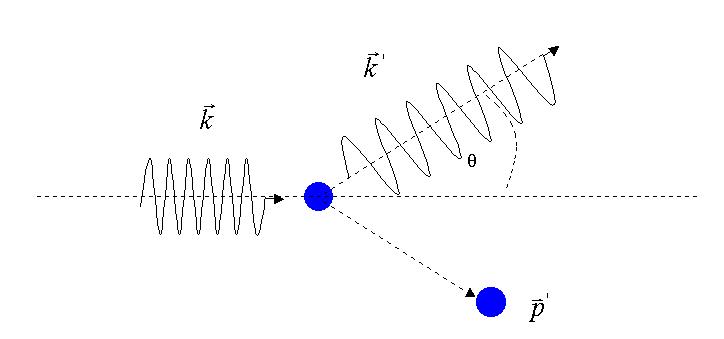
Das einlaufende Photon mit der Wellenlänge
wird an
einem Elektron gestreut. Die Wellenlänge
' nach
dem Streuvorgang ist größer als
, da das Photon
einen Teil seines Impulses und seiner Energie an das Elektron abgegeben hat. Der Wellenzahlvektor k ist gegeben durch 2Pi/
Im Grunde kann man Max Planck (Planck, Max Karl Ernst Ludwig 1858-1947) Geburtshelfer der Quantentheorie bezeichnen. Er fand das berühmte
Plancksche Strahlungsgesetz, welches die Intensität (genauer Energiedichte) des
von einem schwarzen Körpers emittierten elektromagnetischen Spektrums
beschreibt. Lange Zeit, konnte man nur Ausschnitte des Spektrums (im unteren und oberen
Wellenlängenbereich) theoretisch erklären, jedoch nicht den gesamten Verlauf.
Nach vielen ausgerupften Haarbüscheln kam Planck auf die verwegene Idee, das
Licht in Form von Quanten (Energiepakete) zu beschreiben, deren Energie proportional zur Frequenz des
Lichtes ist (
). Damit war es ihm möglich, den gesamten Verlauf des Spektrums zu beschreiben. Wenn Licht nun Teilcheneigenschaften besitzt, warum sollten dann Teilchen nicht Welleneigenschaften besitzen? Eine sehr berechtigte
Frage, deren Antwort weitreichende Konsequenzen mit sich bringt. Werfen wir einen Blick auf die relativistische Energie-Impuls-Beziehung eines Teilchens:
Dabei ist E die Energie, p der Impuls eines Teilchens und m seine Ruhemasse. Nach dem heutigen Stand der Forschung ist
die Ruhemasse eines Lichtteilchens (Photon oder Quant) Null (m = 0). Wenden wir
die Energie-Impuls-Beziehung auf ein Photon an, dann ergibt sich
oder
Der aufmerksame Leser wird sofort bemerkt haben, dass ich eine Lösung, nämlich
unterschlagen habe. Dazu später vielleicht mehr. Nun kennen wir den Zusammenhang zwischen Wellenlänge und Frequenz einer elektromagnetischen Welle:
Damit ergibt sich
Fassen wir die gefundenen extrem wichtigen Beziehungen noch einmal zusammen:
Die letzte Gleichung ist die De Broglie-Beziehung (Broglie, Louis Victor, Herzog 1892-1987). Diese beiden Gleichungen spiegeln den Zusammenhang zwischen Teilcheneigenschaften (Energie E und Impuls p) und Welleneigenschaften (Frequenz
und Wellenlänge
) wieder. Noch sind wir aber nicht am Ziel. Werfen wir einen Blick auf die Maxwellgleichungen, die ja die Ausbreitung
elektromagnetischer Wellen beschreibt. Aus dem Viererpotential
lassen sich elektrische und magnetische Felder ableiten.
genügt der Bewegungsgleichung (Differential- bzw. Wellengleichung)
mit der Eichbedingung
Lösungen der Wellengleichung sind Ebene Wellen (z.B. ergibt die Ausbreitung in x-Richtung):
Setzen wir die Lösung in die Wellengleichung oben ein, erhalten wir
oder die oben eingeführte Beziehung
Jetzt wird’s spannend, differnziert man nämlich die Lösung für
nach der Zeit, ergibt sich
Die Ableitung nach der Zeit ist also proportional zur
Energie. Analog ist die Ableitung nach dem Ort proportional zum Impuls. Wir
wollen nun einen Energie- und Impuls-Operator definieren, dessen Eigenwerte
genau die Energie und den Impuls eines (freien) Teilchens liefert:
Jetzt sind wir so weit, die nicht-relativistische Wellengleichung für ein
„quantenmechanisches“ Teilchen aufzustellen (Sie sehen schon, in welchen
Formulierungsnotstand man aufgrund des Welle-Teilchen-Dualismus gerät). Die
nicht-relativistische Energie-Impulsbeziehung eines Teilchens lautet einfach:
Den übergang zur Quantenmechanik wollen wir nun etwas
schlampig vollziehen, in dem wir einfach Energie und Impuls durch die
entsprechenden Operatoren ersetzen (das Resultat ist trotzdem richtig) und die
Operatorgleichung auf eine Wellenfunktion
anwenden:
Dies ist die berühmte Schrödinger-Gleichung (Schrödinger, Erwin 1887-1961). Die
spannende Frage ist nur, welche physikalische Bedeutung hat die Wellenfunktion
? Darüber wurde lange gerätselt, bis Max
Born (Born, Max 1882-1970) die glänzende Idee hatte, dass nicht der Wellenfunktion
selbst eine physikalische Bedeutung zukommt, sondern dem Absolutquadrat der Wellenfunktion
w ist die Aufenthaltswahrscheinlichkeit-Dichte eines Teilchens. Man kann also
theoretisch nur Wahrscheinlichkeitsaussagen bezüglich des Aufenthaltes eines
Teilchens treffen. Demnach muss die Wahrscheinlichkeit, ein quantenmechanisches
Teilchen irgendwo im Raum anzutreffen Eins sein. Mathematisch gesprochen heißt das
Dabei erstreckt sich die Integration über das gesamte
Volumen V (wenn man so will, ist V das Volumen des Universums, falls das
Teilchen nicht irgendwo eingesperrt ist). In der Quantenmechanik herrscht mindestens genauso viel
Verwirrung wie in der Relativitätstheorie. Viele kurzsichtige Physiker stellen
sich auf den Standpunkt, dass die Quantenmechanik die universellste aller
Theorien ist. Man kann sicher eine Menge Effekte mit Hilfe des Theorieapparates
der Quantenmechanik erklären, die vorher im Dunkeln schlummerten. Jedoch hat
auch die Quantentheorie ihre Grenzen. Auf dem ersten Blick erscheint die
Quantentheorie als merkwürdiges Wahrscheinlichkeitsgebilde. Jedoch gibt es in
der Quantentheorie durchaus streng deterministische Ergebnisse. Es erscheint mir
sinnvoller, die Quantentheorie in zwei Teile zu spalten. Einen statistischen
(Quantenstatistik) und einen deterministischen. Der deterministische Teil beschreibt die isolierten Quantenobjekte, z.B. das
Energiespektrum eines Wasserstoffatoms, welches sich nicht in Wechselwirkung mit
seiner Umgebung befindet. Die Energieniveaus des Wasserstoffatoms lassen sich
exakt berechnen und von Wahrscheinlichkeiten kann nicht im entferntesten die
Rede sein. Sie werfen natürlich berechtigt ein, wie man nun Kenntnis von der
Lage der Energieniveaus erhalten soll, wenn keine Wechselwirkung mit der
Umgebung stattfindet. Dazu müssen wir das Wasserstoffatom stören und ein wenig
an ihm rütteln. Z.B. durch „Anregung“ des Elektrons auf ein höheres Energieniveau und „Abregung“ des Elektrons durch Abstrahlung eines Photons, welches
genau die Energiedifferenz zwischen End- und Anfangsniveau mit sich trägt.
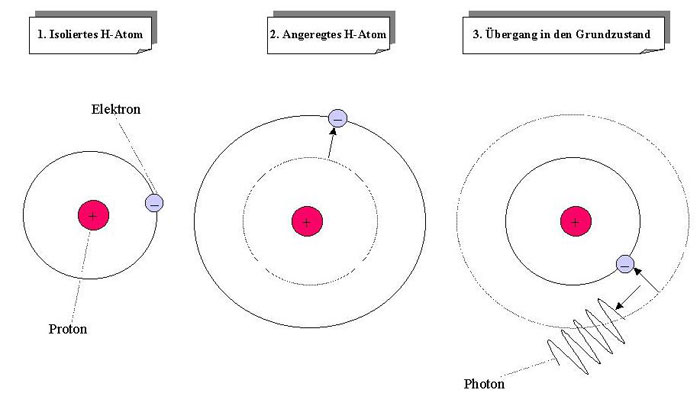
Stört man das Wasserstoffatom, und jeder experimentelle
Eingriff ist eine Störung, befreit man es sozusagen aus seiner Isolationshaft
und die Quantenstatistik kommt ins Spiel. Man kann nämlich nur eine mittlere
Lebensdauer bezüglich des Aufenthalts des Elektrons auf dem höheren
Energieniveau angeben, d.h. man weiß nicht genau, wann es in den Grundzustand
übergeht. Misst man die Zeiten vieler übergänge und bildet den Mittelwert,
erhält man die mittlere Lebensdauer, welche man wiederum mit Hilfe der
Quantenstatistik genau berechnen kann. Es gibt in der Quantenmechanik unglaubliche Effekte.
Einer der merkwürdigsten ist der Tunneleffekt. Stellen Sie sich vor, sie werfen
einen Tennisball gegen die Wand. Kaum einer wundert sich darüber, dass dieser
von der Wand abprallt. In der Quantenmechanik gibt es jedoch eine
Wahrscheinlichkeit dafür, dass der Tennisball durch die Wand hindurchtunnelt. Gäbe
es diesen Effekt nicht, gäbe es uns nicht. Die Sonne funktioniert nach dem
Prinzip der Kernfusion, d.h. positive leichte Kerne verschmelzen zu schwereren. Da sich aber positive Kerne abstoßen, und die Kernkräfte
erst bei sehr kurzen Abständen zu wirken beginnen, dürfte es zu keiner Fusion
kommen, da die elektrische Abstoßung eine Annäherung der Kerne verhindert. Mit
Hilfe des Tunneleffekts gelingt es den Teilchen jedoch, die Potentialbarriere zu
durchdringen und in den Wirkungsbereich der Kernkräfte zu gelangen. Selbstverständlich kann man auch eine relativistische
(quantenmechanische) Wellengleichung aufstellen. Beispiele dafür sind die Klein-Gordon-Gleichung und die Diracgleichung.
Jedoch tauchen bei der relativistischen Betrachtung von quantenmechanischen
Teilchen weitere Probleme auf. Ist z.B. die kinetische Energie groß genug, um
ein Teilchen-Antiteilchen-Paar zu erzeugen, kann es zur
Teilchen-Antiteilchen-Paar-Bildung kommen. Die Rechnereien, die zur Beschreibung
derartiger Effekte notwendig sind, können sich sehr wohl mit der
Kompliziertheit der Einsteinschen Feldgleichungen messen. Ich hoffe hier einen kurzen wenig vernebelten Einblick in
die Quantenmechanik gewährt zu haben. Der Arm der Relativitätstheorie reicht
sogar bis in die Tiefen der Quantentheorie. Ohne Einsteins berühmte Formel
E = mc2
läuft in der Physik kaum etwas.
Home
Andere Theorien