Einsteins Erben: Weltmodelle der Allgemeinen Relativitaetstheorie

Wir wollen in diesem Kapitel so verwegen sein und die Einsteinschen Feldgleichungen auf das Universum anwenden. Dabei werde ich so gut es geht von unnötigem Formelkram Abstand nehmen und mich im wesentlichen auf die Diskussion der Ergebnisse beschränken. Um überhaupt etwas ausrechnen zu können, ist es erforderlich das Problem auf sinnvolle aber noch allgemeingültige Weise zu vereinfachen. Wie immer muss man einen sinnvollen Ansatz für die Metrik finden. Der hier vorgestellte Ansatz geht davon aus, dass das Universum im Mittel homogen und isotrop ist, also die Massendichte als konstant angenommen werden darf (dies ist durchaus gerechtfertigt, wenn man über viele Galaxien mittelt) und keine Richtung gegenüber einer anderen bevorzugt werden darf. D.h. Gleichberechtigung total. Dieser Sachverhalt bezeichnet man auch als das Kosmologische Prinzip: Im Universum sind alle Positionen und Richtungen gleichwertig Diese Annahmen sind jedoch mit Vorsicht zu genießen, da sie sich nur auf den sichtbaren Bereich des Universums beziehen. Dunkle Materie (also Materie, die kaum ein Photon abstrahlt) wird nicht mit einbezogen. Wir erkennen schon an dieser Stelle, dass eine große Unsicherheit in die Massendichte

eingeht. Es ist ja auch ein wenig schwierig, das Universum mal eben auf die Badezimmerwaage zu stellen. Die Metrik, die dem Kosmologischen Prinzip genügt ist die Robertson-Walker-Metrik:

Die Metrik hängt von der Konstanten k ab, wobei man die Fälle: k = +1, k = 0, k = -1 auseinanderhalten muss. Alle räumlichen Abstände zwischen zwei Punkten sind proportional zu R(t), dies gilt insbesondere für den Abstand zwischen zwei Galaxien. Die Größe R(t) wird daher kosmischer Skalenfaktor genannt. Für k = +/-1 ist R(t) der Krümmungsradius des Universums, insbesondere für k = +1 der Radius des Universums selbst. Wir erkennen für k = 0 die ähnlichkeit mit der Metrik für ein kugelsymmetrisches Problem. Das soll uns erst einmal genügen, was den Ansatz für die Metrik zur Beschreibung des Universums angeht. Damit ist das Päckchen an Vorab-überlegungen aber noch nicht geschnürt. Wenden wir uns nun den Einsteinschen Feldgleichungen zu.

Die hier eingeführte Kosmologische Konstante

, die zuerst Einsteins Hirn entsprungen ist, stellt eine Erweiterung der Feldgleichnungen dar, die mit den notwendigen Symmetrieprinzipien und Erhaltungssätzen vereinbar ist. Damit die Verhältnisse in unserem Sonnensystem richtig beschrieben werden können, muss

einen sehr kleinen Wert besitzen, der aber für die Dynamik des Kosmos sehr wohl von Bedeutung sein kann. Ein Blick auf die Feldgleichungen verrät uns sofort, was noch einer Klärung bedarf, nämlich der Energie-Impuls-Tensor. Die Materie des Universums betrachten wir im Großen und im Mittel als kontinuierliche, ideale Flüssigkeit mit dem Energie-Impuls-Tensor

Die Massendichte

und der Druck P werden als räumlich homogen angesehen, d.h. P = P (t) und

(t). Dass P und

von der Zeit abhängen müssen, ist klar. Man stelle sich einen Luftballon gefüllt mit na eben Luft vor. Dieser Luftballon hat ein Volumen V und ist gefüllt mit der Gasmasse m. Bringen wir diesen Luftballon ins All, wird er sich ausdehnen. Die Gasmasse bleibt dabei im Ballon unverändert, sein Volumen vergrößert sich aber und damit nimmt die Dichte im Ballon ab, da Dichte gegeben ist durch masse geteilt durch Volumen. Expandiert nun das Universum z.B. bleibt die Gesamtmasse des Universums erhalten, das Volumen wächst aber, der Balloneffekt! Ein großer Unsicherheitsfaktor bei der Bestimmung der massendichte des Universums ist die dunkle Materie. Dieser finstere Teil der All-Masse kann wesentliche Beiträge zur Dichte ausmachen. Mögliche Quellen sind:

abgekühlte weiße und braune Zwerge
massive Neutrinos
supermassive Schwarze Löcher

Einen Teil dieser dunklen Materie kann man aufgrund ihres gravitativen Einflusses auf leuchtende Materie bestimmen. Man denke nur an Schwarze Löcher im Zentrum von Galaxien. Wir wollen uns noch ein paar Gedanken zur Kosmologischen Konstanten L machen. Die Kosmologische Konstante kann man als Energiedichte des Vakuums interpretieren. Eine Abschätzung für

kann man demnach aus der Quantenfeldtheorie erhalten. Anstrengende überlegungen zu dieser Problematik ergeben, dass die Annahme

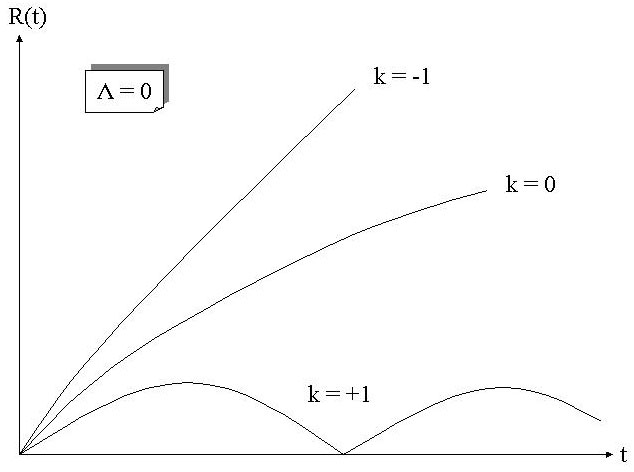
= 0 naheliegend ist. Damit ergeben sich für den kosmologischen Skalenfaktor R(t) folgende Lösungen in Abhängigkeit von k:

Die Weltmodelle mit k = -1 oder 0 haben eine unendliche Ausdehnung. Für k = 0 geht die Geschwindigkeit der Expansion langsam gegen Null, für k = -1 gegen eine Konstante. Das Weltmodell mit k = 0 heißt Einstein-de-Sitter-Universum. Für k = 1 erhalten wir eine periodische Bewegung, d.h. die Expansion erreicht einen maximalen Wert und danach das Universum fällt wieder auf eine Singularität zusammen. Danach beginnt wieder alles von vorne. Die Lösungen für k = 0 und k = -1 bezeichnet man auch als offene Lösungen. Das Universum expandiert immer weiter, bis alle Sterne erloschen sind, keine lebensnotwendige Energie mehr vorhanden ist. Das Universum wird zu einer riesigen Leichenhalle. Es ist bis heute noch nicht eindeutig geklärt, wohin sich das Universum entwickelt. Den Anhängern der Wiedergeburt dürfte die k = +1 Lösung wohl am besten schmecken. Für die katholische Kirche, die von der Existenz der Ewigkeit ausgeht, kämen die anderen beiden Lösungen in Frage. Alle experimentellen Beobachtungen sprechen derzeit dafür, dass das All sich beschleunigt ausdehnt.